MATEMÁTICA: maio 2020

Retas paralelas são aquelas que não se interceptam em nenhum ponto. Uma reta é transversal à outra se ambas apresentam apenas um ponto em comum. Ao traçarmos duas retas r e s, tal que r // s (“r é paralela a s”), e também uma reta transversal t que intercepte r e s, haverá a formação de oito ângulos. Na imagem a seguir, identificamos esses ângulos por a, b, c, d, e, f, g, h.

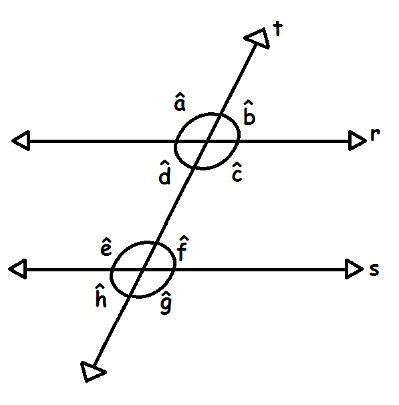
A interseção da reta t com as retas paralelas r e s deu origem aos ângulos a, b, c, d, e, f, g, h

Experimente fazer um desenho semelhante a esse que foi mostrado de duas retas paralelas cortadas por uma transversal. Ao finalizar seu desenho, divida-o ao meio, cortando-o entre as retas paralelas. Se você colocar os ângulos formados pelas retas s e t exatamente em cima dos ângulos formados pelas retas r e s, observará que eles são exatamente iguais.

Podemos classificar os ângulos formados por duas retas paralelas cortadas por uma transversal de acordo com a posição desses ângulos. Se eles estiverem entre as retas paralelas, dizemos que esses ângulos são internos; caso contrário, dizemos que eles são externos. Na figura a seguir, os ângulos externos estão na faixa azul, enquanto os ângulos internos estão na faixa amarela. Ao analisarmos dois ângulos, eles podem estar do mesmo lado ou em lados alternados em relação à reta transversal. Se dois ângulos estão à direita ou ambos estão à esquerda da reta t, dizemos que esses ângulos são colaterais; mas se estão em lados alternados, um à direita, e o outro à esquerda, dizemos que esses ângulos são alternos.

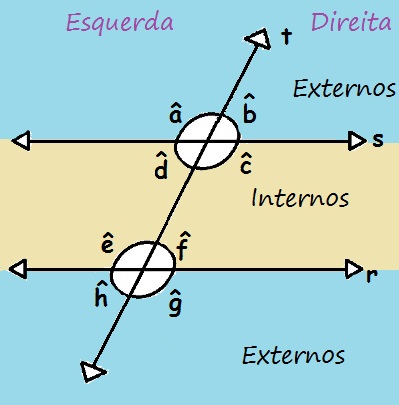
Os ângulos podem ser classificados como internos ou externos, e dois ângulos podem ser colaterais ou alternos

Sabendo que os ângulos formados pelas retas r e t são iguais aos formados pelas retas s e t, podemos afirmar que os pares de ângulos abaixo são correspondentes:

· a e e

· b e f

· c e g

· d e h

Estes pares de ângulos colaterais correspondentes, acima mencionados, possuem a mesma medida. Mas sabemos que os ângulos opostos pelo vértice são congruentes, isto é, também possuem a mesma medida. Então, podemos dizer que:

· a = c = e = g

· b = d = f = h

Os ângulos d e f e também e e c podem ser classificados como ângulos alternos internos, pois estão na região interna e em lados alternados. Os ângulos d e e, bem como os c e f, podem ser classificados como ângulos colaterais internos, uma vez que estão na região interna e do mesmo lado em relação à reta t.

Semelhantemente, os ângulos a e h, assim como b e g, são ângulos colaterais externos, pois estão na região externa e do mesmo lado em relação à reta t. Assim como os ângulos a e g, bem como b e h, são ângulos alternos externos, pois estão na região externa e em lados alternados em relação à reta transversal t.

Na figura a seguir, podemos ver claramente os ângulos alternos internos, colaterais internos, alternos externos e colaterais externos formados através de duas retas paralelas cortadas por uma transversal:

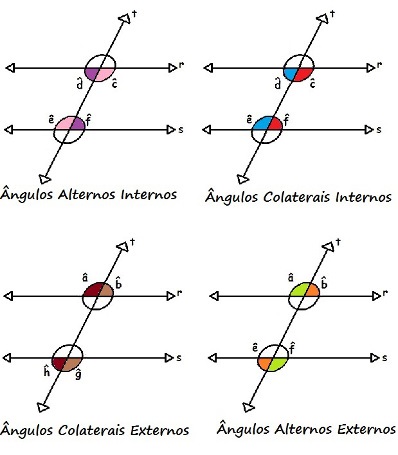
Duas retas paralelas cortadas por uma transversal formam ângulos alternos internos, colaterais internos, alternos externos e colaterais externos

11-15 de Maio Material de Apoio- Proporcionalidade 9° ano (Matemática)

Material de apoio 9° Ano Matemática

Proporcionalidade entre Grandezas

Definimos por grandeza tudo aquilo que pode ser contado e medido, como o tempo, a velocidade, comprimento, preço, idade, temperatura entre outros. As grandezas são classificadas em: diretamente proporcionais e inversamente proporcionais.

Grandezas diretamente proporcionais

São aquelas grandezas onde a variação de uma provoca a variação da outra numa mesma razão. Se uma dobra a outra dobra, se uma triplica a outra triplica, se uma é divida em duas partes iguais a outra também é divida à metade.

Exemplo 1

Se três cadernos custam R$ 8,00, o preço de seis cadernos custará R$ 16,00. Observe que se dobramos o número de cadernos também dobramos o valor dos cadernos. Confira pela tabela:

Exemplo 2

Para percorrer 300 km, um carro gastou 30 litros de combustível. Nas mesmas condições, quantos quilômetros o carro percorrerá com 60 litros? E com 120 litros?

Grandezas inversamente proporcionais

Uma grandeza é inversamente proporcional quando operações inversas são utilizadas nas grandezas. Por exemplo, se dobramos uma das grandezas temos que dividir a outra por dois, se triplicamos uma delas devemos dividir a outra por três e assim sucessivamente. A velocidade e o tempo são considerados grandezas inversas, pois aumentarmos a velocidade, o tempo é reduzido, e se diminuímos a velocidade, o tempo aumenta.

Exemplo 3

Para encher um tanque são necessárias 30 vasilhas de 6 litros cada uma. Se forem usadas vasilhas de 3 litros cada, quantas serão necessárias?

Utilizaremos 60 vasilhas, pois se a capacidade da vasilha diminui, o número de vasilhas aumenta no intuito de encher o tanque.

As duas grandezas são muito utilizadas em situações de comparação, isto é comum no cotidiano. A utilização da regra de três nos casos envolvendo proporcionalidade direta e inversa é de extrema importância para a obtenção dos resultados.

sábado, 9 de maio de 2020

VÍDEOS CENTRO DE MÍDIAS 2° ANO

https://www.youtube.com/watch?v=8BzMzV-D_3s&feature=emb_logo (04/05)

https://www.youtube.com/watch?v=c_nbqUzB5SQ&feature=emb_logo (06/05)

MATERIAL DE APOIO 2° ANO A E B (MATEMÁTICA)

MATERIAL DE APOIO 2° ANO A E B

O Círculo Trigonométrico, também chamado de Ciclo ou Circunferência Trigonométrica, é uma representação gráfica que auxilia no cálculo das razões trigonométricas.

Radianos do Círculo Trigonométrico

A medida de um arco no círculo trigonométrico pode ser dada em grau (°) ou radiano (rad).

· 1° corresponde a 1/360 da circunferência. A circunferência é dividida em 360 partes iguais ligadas ao centro, sendo que cada uma delas apresenta um ângulo que corresponde a 1°.

· 1 radiano corresponde à medida de um arco da circunferência, cujo comprimento é igual ao raio da circunferência do arco que será medido.

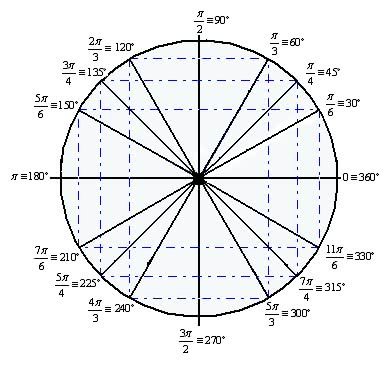
Para auxiliar nas medidas, confira abaixo algumas relações entre graus e radianos:

· π rad = 180°

· 2π rad = 360°

· π/2 rad = 90°

· π/3 rad = 60°

· π/4 rad = 45°

Obs: Se quiser converter essas unidades de medidas (grau e radiano) utiliza-se a regra de três.

Exemplo: Qual a medida de um ângulo de 30° em radianos?

π rad -180°
x – 30°
x = 30° . π rad/180°
x = π/6 rad

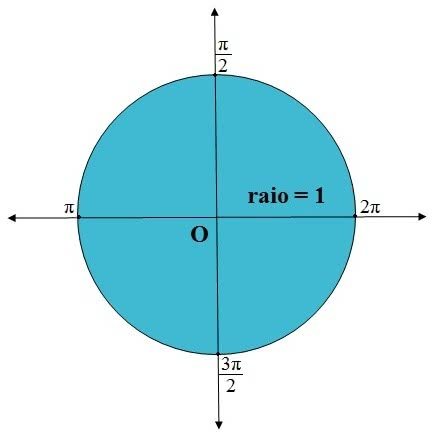
Quadrantes do Círculo Trigonométrico

Quando dividimos o círculo trigonométrico em quatro partes iguais, temos os quatro quadrantes que o constituem. Para compreender melhor, observe a figura abaixo:

FIGURA

· 1.° Quadrante: 0º

· 2.° Quadrante: 90º

· 3.° Quadrante: 180º

· 4.° Quadrante: 270º

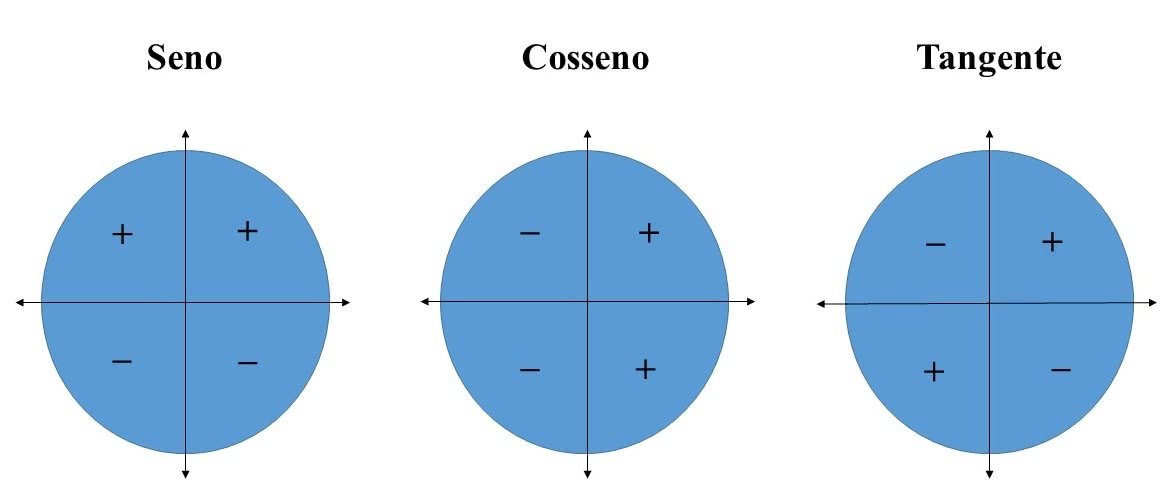
Círculo Trigonométrico e seus Sinais

De acordo com o quadrante em que está inserido, os valores do seno, cosseno e tangente variam.

Ou seja, os ângulos podem apresentar um valor positivo ou negativo.

Para compreender melhor, veja a figura abaixo:

Como Fazer o Círculo Trigonométrico?

Para fazer um círculo trigonométrico, devemos construí-lo sobre o eixo de coordenadas cartesianas com centro em O. Ele apresenta um raio unitário e os quatro quadrantes.

Razões Trigonométricas

As razões trigonométricas estão associadas às medidas dos ângulos de um triângulo retângulo.

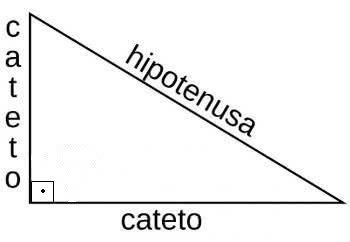
Representação do triângulo retângulo com seus catetos e a hipotenusa

Elas são definidas pelas razões de dois lados de um triângulo retângulo e do ângulo que forma, sendo classificadas em seis maneiras:

Seno (sen)

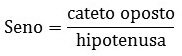
Lê-se cateto oposto sobre a hipotenusa.

Cosseno (cos)

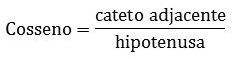
Lê-se cateto adjacente sobre a hipotenusa.

Tangente (tan)

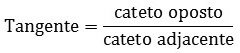
Lê-se cateto oposto sobre cateto adjacente.

ATIVIDADE 2° ANO A E B (MATEMÁTICA)

ROTEIRO DE ESTUDOS

Professor: Helder	Disciplina: Matemática 2° A e B
Tempo para execução: 45 minutos	Instrumento de verificação da aprendizagem: Aulas do Centro de Mídias
Quantidade de aulas: 3 aulas	Semana de : 04-08 de Maio
Prazo para entrega: 15/05	Opções de Entrega: Email, grupo de Wathsapp
Habilidades: Conhecer as principais características das funções trigonométricas básicas (especialmente o seno, o cosseno e a tangente), sabendo construir seus gráficos e aplicá-las em diversos contextos
Tema/Conteúdo: Círculo Trigonométrico/Relações métricas no triângulo retângulo
1) Observe o Círculo Trigonométrico a seguir: Os ângulos de 45°; 135°;240°;330° estão em quais quadrantes? 2) Transforme os ângulo abaixo em radianos: a) 120° b) 160° 3) Encontre os valores do seno, cosseno e tangente do ângulo α no triângulo abaixo:

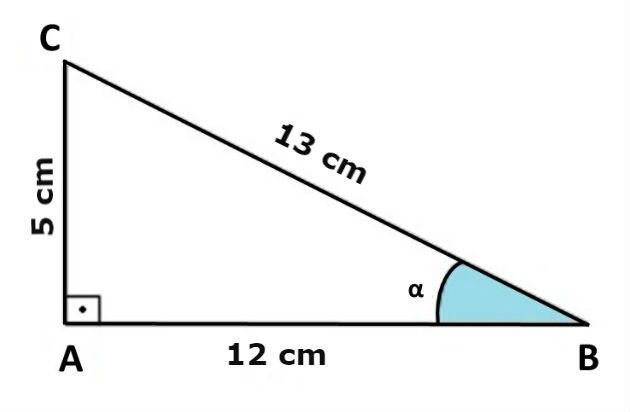sexta-feira, 8 de maio de 2020

VÍDEO EXTRA P.A E P.G 1° ANO

https://www.youtube.com/watch?v=zoFC82aPq1A

VÍDEOS CENTRO DE MÍDIAS 1°A

https://www.youtube.com/watch?v=DZJRAQQX-Ys&feature=emb_logo (27/04)

https://www.youtube.com/watch?v=ebbqcThdliI&feature=emb_logo (04/05)

https://www.youtube.com/watch?v=Vk035p3GROE&feature=emb_logo (06/05)

ATIVIDADE 1° ANO A (MATEMÁTICA)

Tema/Conteúdo: PROGRESSÃO ARITMÉTICA (P.A); PROGRESSÃO GEOMÉTRICA; MÉDIA, MODA E MEDIANA

Atividade

1) Considere a seguinte sequência de números:

I. 3,7,11...
II. 2,6,18...
III. 2, 5, 10, 17, …

O número que continua cada uma das sequências na ordem dada deve ser respectivamente:

2) Enem – 2013 (Adaptado) As projeções para a produção de arroz no período de 2012 - 2021, em uma determinada região produtora, apontam para uma perspectiva de crescimento constante da produção anual. O quadro apresenta a quantidade de arroz, em toneladas, que será produzida nos primeiros anos desse período, de acordo com essa projeção.

No período de 2012 a 2021 temos 10 anos, com esses dados calcule o valor do 10° termo.

3) Encontre o 15º (décimo quinto) termo da progressão aritmética: (1, 4, 7, 10, 13, 16, …)

4) Calcule o quarto e o sétimo termos da P. G. (3, -6, 12, …).

5) Determine a média, moda e mediana do seguinte conjunto de dados:

A = {2, 5, 1, 8, 12, 9, 10, 2}

DESAFIO:

Na figura 1, há 1 triângulo.

Na figura 2, o número de triângulos menores é 4.

Na figura 3, o número de triângulos menores é 16 e assim por diante.

Prosseguindo essa construção de figuras, teremos quantos triângulos menores na figura 7?

Fórmulas Utilizadas:

a_n = a₁ + (n – 1) . r Progressão Aritmética

a_n = a₁ . q^{n – 1}

Progressão Geométrica

MATERIAL DE APOIO 1° ANO A (MATEMÁTICA)

MATERIAL DE APOIO MATEMÁTICA REFERENTE AS AULAS DADAS NO CENTRO DE MÍDIA (1° A-MATEMÁTICA)

PROGRESSÃO ARITMÉTICA (P.A)

A Progressão Aritmética (P.A.) é uma sequência de números onde a diferença entre dois termos consecutivos é sempre a mesma. Essa diferença constante é chamada de razão da P.A..

Sendo assim, a partir do segundo elemento da sequência, os números que surgem são resultantes da soma da constante com o valor do elemento anterior.

Isso é o que a diferencia da progressão geométrica (P.G.), pois nesta, os números são multiplicados pela razão, enquanto na progressão aritmética, eles são somados.

As progressões aritméticas podem apresentar um número determinado de termos (P.A. finita) ou um número infinito de termos (P.A. infinita).

Para indicar que uma sequência continua indefinidamente utilizamos reticências, por exemplo:

· a sequência (4, 7, 10, 13, 16, ...) é uma P.A. infinita.

· a sequência (70, 60, 50, 40, 30, 20, 10) é uma P.A. finita.

Cada termo de uma P.A. é identificado pela posição que ocupa na sequência e para representar cada termo utilizamos uma letra (normalmente a letra a) seguida de um número que indica sua posição na sequência.

Por exemplo, o termo a₄ na P.A (2, 4, 6, 8, 10) é o número 8, pois é o número que ocupa a 4ª posição na sequência.

Classificação de uma P.A.

De acordo com o valor da razão, as progressões aritméticas são classificadas em:

· Constante: quando a razão for igual a zero. Por exemplo: (4, 4, 4, 4, 4...), sendo r = 0.

· Crescente: quando a razão for maior que zero. Por exemplo: (2, 4, 6, 8,10...), sendo r = 2.

· Decrescente: quando a razão for menor que zero (15, 10, 5, 0, - 5,...), sendo r = - 5

Fórmula do Termo Geral

Esse cálculo é expresso através da fórmula do termo geral da P.A., que nos permite conhecer qualquer elemento de uma progressão aritmética. Assim, temos:

Python Progressivo: Progressão Aritmética (PA) em Python

Onde,

a_n: termo que queremos calcular
a₁: primeiro termo da P.A.
n: posição do termo que queremos descobrir
r: razão

Exemplo

Calcule o 10° termo da P.A.: (26, 31, 36, 41, ...)

Solução

Primeiro, devemos identificar que a₁ = 26, r = 31 - 26 = 5 e n = 10 (10º termo). Substituindo esses valores na fórmula do termo geral, temos:

a_n = a₁ + (n - 1) . r
a₁₀ = 26 + (10-1) . 5
a₁₀ = 26 + 9 .5
a₁₀ = 71

Portanto, o décimo termo da progressão aritmética indicada é igual a 71.

PROGRESSÃO GEOMÉTRICA (P.G)

Progressão Geométrica (PG) corresponde a uma sequência numérica cujo quociente (q) ou razão entre um número e outro (exceto o primeiro) é sempre igual.

Em outras palavras, o número multiplicado pela razão (q) estabelecida na sequência, corresponderá ao próximo número, por exemplo:

PG: (2,4,8,16, 32, 64, 128, 256...)

No exemplo acima, podemos constatar que na razão ou quociente (q) da PG entre os números, o número que multiplicado pela razão (q) determina seu consecutivo, é o número 2:

2 . 2 = 4

4 . 2 = 8

8 . 2 = 16

16 . 2 = 32

32 . 2 = 64

64 . 2 = 128

128 . 2 = 256

Vale lembrar que a razão de uma PG é sempre constante e pode ser qualquer número racional (positivos, negativos, frações) exceto o número zero (0).

Classificação das Progressões Geométricas

De acordo com o valor da razão (q), podemos dividir as Progressões Geométricas (PG) em 4 tipos:

PG Crescente

Na PG crescente a razão é sempre positiva (q > 0) formada por números crescentes, por exemplo:

(1, 3, 9, 27, 81, ...), onde q = 3

PG Decrescente

Na PG decrescente, a razão é sempre positiva (q > 0) e diferente de zero (0) formada por números decrescentes.

Ou seja, os números da sequência são sempre menores do que seus antecessores, por exemplo:

(-1, -3, -9, -27, -81, ...) onde q = 3

PG Oscilante

Na PG oscilante, a razão é negativa (q < 0), formada por números negativos e positivos, por exemplo:

(3,-6,12,-24,48,-96,192,-384,768,...), onde q = -2

PG Constante

Na PG constante, a razão é sempre igual a 1 formada pelos mesmos números a, por exemplo:

(5, 5, 5, 5, 5, 5, 5, ...) onde q = 1

Fórmula do Termo Geral

Para encontrar qualquer elemento da PG, utiliza-se a expressão:

a_n = a₁ . q^(n-1)

Onde:

a_n: número que queremos obter
a₁: o primeiro número da sequência
q^(n-1): razão elevada ao número que queremos obter, menos 1

Assim, para identificar o termo 20 de uma PG de razão q = 2 e número inicial 2, calcula-se:

PG: (2,4,8,16, 32, 64, 128,...)

a₂₀ = 2 . 2^(20-1)

a₂₀ = 2 . 2¹⁹

a₂₀ = 1048576