MATERIAL DE APOIO 2° ANO A E B
O Círculo
Trigonométrico, também chamado de Ciclo ou Circunferência
Trigonométrica, é uma representação gráfica que auxilia no cálculo das razões
trigonométricas.
Radianos do Círculo
Trigonométrico
A medida de um arco no círculo trigonométrico pode ser dada em grau (°)
ou radiano (rad).
·
1° corresponde a 1/360 da
circunferência. A circunferência é dividida em 360 partes iguais ligadas ao
centro, sendo que cada uma delas apresenta um ângulo que corresponde a 1°.
·
1 radiano corresponde à medida de um arco
da circunferência, cujo comprimento é igual ao raio da circunferência do arco
que será medido.
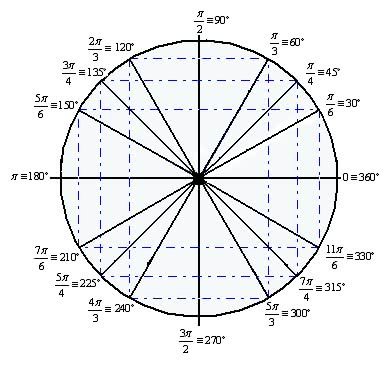
Para auxiliar nas medidas, confira abaixo algumas relações entre graus e
radianos:
·
π rad = 180°
·
2π rad = 360°
·
π/2 rad = 90°
·
π/3 rad = 60°
·
π/4 rad = 45°
Exemplo: Qual a medida de
um ângulo de 30° em radianos?
π rad -180°
x – 30°
x = 30° . π rad/180°
x = π/6 rad
x – 30°
x = 30° . π rad/180°
x = π/6 rad
Quadrantes do Círculo Trigonométrico
Quando dividimos o círculo trigonométrico em quatro partes
iguais, temos os quatro quadrantes que o constituem. Para
compreender melhor, observe a figura abaixo:
FIGURA
·
1.° Quadrante: 0º
·
2.° Quadrante: 90º
·
3.° Quadrante: 180º
·
4.° Quadrante: 270º
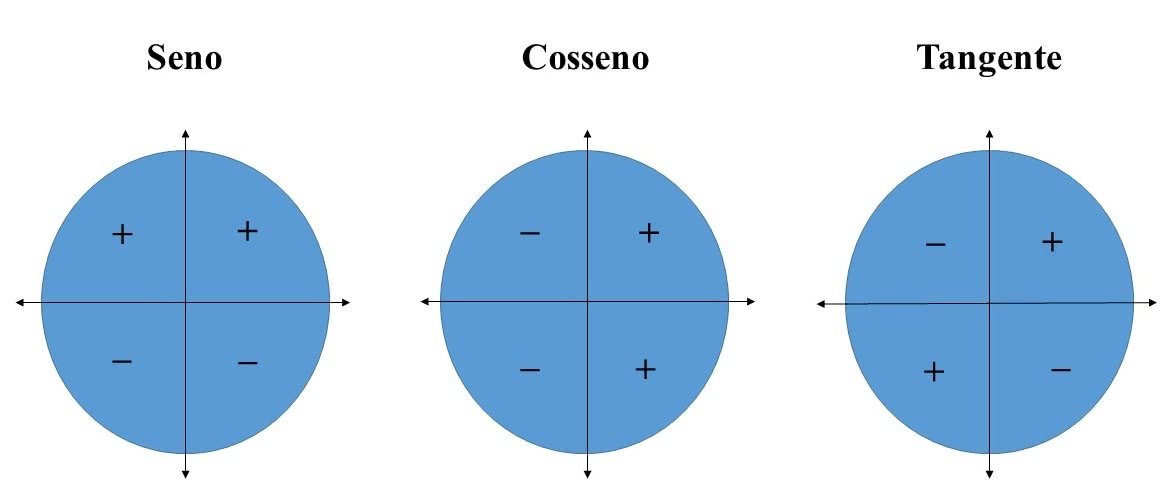
Círculo
Trigonométrico e seus Sinais
De acordo com o quadrante em que está inserido, os valores do seno,
cosseno e tangente variam.
Ou seja, os ângulos podem apresentar um valor positivo ou negativo.
Para compreender melhor, veja a figura abaixo:
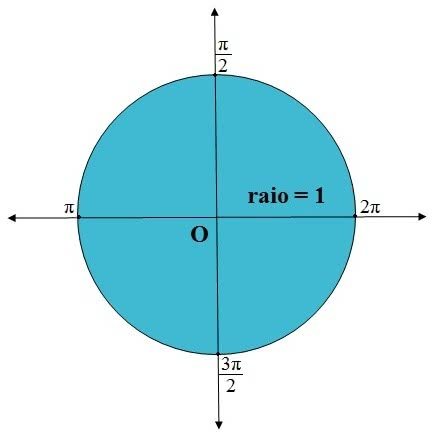
Como Fazer o Círculo Trigonométrico?
Para fazer um círculo trigonométrico, devemos construí-lo sobre
o eixo de coordenadas cartesianas com centro em O. Ele apresenta um raio
unitário e os quatro quadrantes.
Razões Trigonométricas
As razões
trigonométricas estão associadas às medidas dos ângulos de um
triângulo retângulo.
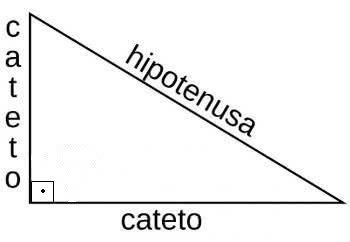
Representação do triângulo retângulo com seus catetos e a
hipotenusa
Elas são definidas pelas razões de dois lados de um triângulo
retângulo e do ângulo que forma, sendo classificadas em seis
maneiras:
Seno (sen)
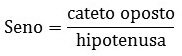
Lê-se cateto oposto sobre a hipotenusa.
Cosseno (cos)
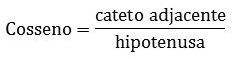
Lê-se cateto adjacente sobre a hipotenusa.
Tangente (tan)
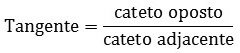
Lê-se cateto oposto sobre cateto adjacente.


Nenhum comentário:
Postar um comentário