NÚMEROS IRRACIONAIS
Os Números Irracionais são números decimais, infinitos e não-periódicos e não podem ser representados por meio de frações irredutíveis.
Interessante notar que a descoberta dos números irracionais foi considerada um marco nos estudos da geometria. Isso porque preencheu lacunas, como por exemplo, a medida da diagonal de um quadrado de lado igual a 1.
Como a diagonal divide o quadrado em dois triângulos retângulos, podemos calcular essa medida usando o Teorema de Pitágoras.

A medida da diagonal desse quadrado será √2. O problema é que o resultado desta raiz é um número decimal infinito e não periódico.
Por mais que tentemos encontrar um valor exato, só conseguimos aproximações deste valor. Considerando 12 casas decimais essa raiz pode ser escrita como:
√2 = 1,414213562373....
Alguns exemplos de irracionais:
· √3 = 1,732050807568....
· √5 = 2,236067977499...
· √7 = 2,645751311064...
PRESTE ATENÇÃO: Diferente dos números irracionais, as dízimas periódicas são números racionais. Apesar de apresentarem uma representação decimal infinita, podem ser representados por meio de frações.
A parte decimal que compõe uma dízima periódica apresenta um período, ou seja, possui sempre a mesma sequência de repetição.
Por exemplo, o número 0,3333... pode ser escrito na forma de fração irredutível, pois:
0,33333=1/3
Portanto, as dízimas periódicas não são números irracionais.
CURIOSIDADES: Número Pi (p)
Identificado como um dos irracionais mais famosos, o número pi é o resultado da divisão entre o perímetro de uma circunferência e seu próprio diâmetro, sendo o valor aproximado igual a 3,14.
Número de Neper (℮)
Também conhecido como constante exponencial, o número de Neper serve de base para os logaritmos naturais. Irracional e da categoria transcendente, seu valor aproximado é de 2,718281.
Número Áureo (F)
Também chamado de número de ouro, é uma constante algébrica simbolizada pela letra grega Phi. Com valor aproximado igual a 1,61803, tornou-se foco de estudo da matemática por ser usado desde a Antiguidade em vertentes artísticas, especialmente nas pinturas renascentistas. Além disso, acredita-se que o número mantém relações com os elementos da natureza.
Você sabia?
• As operações de soma, subtração, multiplicação e divisão entre irracionais podem resultar em valores racionais. Exemplos: √2 + (1 – √2) = 1; √6.√6 = √36 = 6; √10/√2 = 5.
• O número transcendente áureo (número de Euler) também surge da relação numérica presente na sequência de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, 34, 55...). Assim, começando pelo 1, essa sequência é formada somando cada numeral com o numeral que o antecede. No caso do 1, repete-se esse numeral e soma-se, ou seja, 1 + 1 = 2.
De seguida soma-se o resultado com o numeral que o antecede, ou seja, 2 + 1 = 3 e assim sucessivamente, numa sequência infinita:
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
13 + 8 = 21
21 + 13 = 34
34 + 21 = 55
55 + 34 = 89
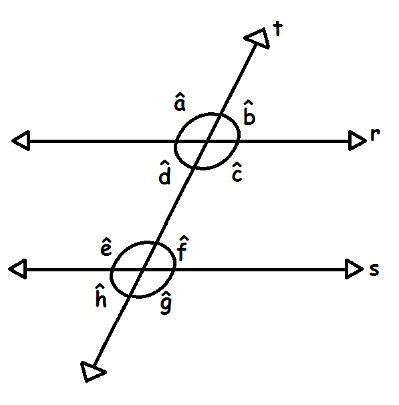
A interseção da reta t com as retas paralelas r e s deu origem aos ângulos a, b, c, d, e, f, g, h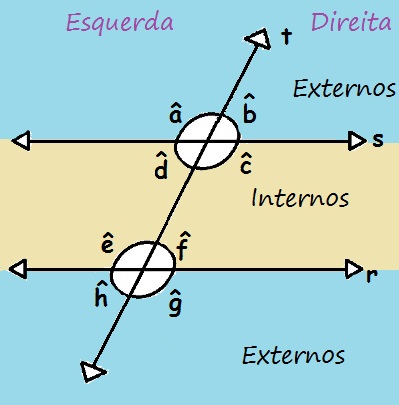
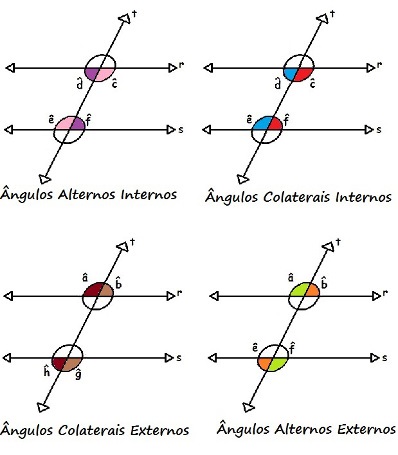
Duas retas paralelas cortadas por uma transversal formam ângulos alternos internos, colaterais internos, alternos externos e colaterais externos
Teorema de Tales
5 + 3 = 8
8 + 5 = 13
13 + 8 = 21
21 + 13 = 34
34 + 21 = 55
55 + 34 = 89
Retas paralelas cortadas por uma transversal
Retas paralelas são aquelas que não se interceptam em nenhum ponto. Uma reta é transversal à outra se ambas apresentam apenas um ponto em comum. Ao traçarmos duas retas r e s, tal que r // s (“r é paralela a s”), e também uma reta transversal t que intercepte r e s, haverá a formação de oito ângulos. Na imagem a seguir, identificamos esses ângulos por a, b, c, d, e, f, g, h.

A interseção da reta t com as retas paralelas r e s deu origem aos ângulos a, b, c, d, e, f, g, h
Experimente fazer um desenho semelhante a esse que foi mostrado de duas retas paralelas cortadas por uma transversal. Ao finalizar seu desenho, divida-o ao meio, cortando-o entre as retas paralelas. Se você colocar os ângulos formados pelas retas s e t exatamente em cima dos ângulos formados pelas retas r e s, observará que eles são exatamente iguais.
Podemos classificar os ângulos formados por duas retas paralelas cortadas por uma transversal de acordo com a posição desses ângulos. Se eles estiverem entre as retas paralelas, dizemos que esses ângulos são internos; caso contrário, dizemos que eles são externos. Na figura a seguir, os ângulos externos estão na faixa azul, enquanto os ângulos internos estão na faixa amarela. Ao analisarmos dois ângulos, eles podem estar do mesmo lado ou em lados alternados em relação à reta transversal. Se dois ângulos estão à direita ou ambos estão à esquerda da reta t, dizemos que esses ângulos são colaterais; mas se estão em lados alternados, um à direita, e o outro à esquerda, dizemos que esses ângulos são alternos.

Os ângulos podem ser classificados como internos ou externos, e dois ângulos podem ser colaterais ou alternos
Sabendo que os ângulos formados pelas retas r e t são iguais aos formados pelas retas s e t, podemos afirmar que os pares de ângulos abaixo são correspondentes:
· a e e
· b e f
· c e g
· d e h
Estes pares de ângulos colaterais correspondentes, acima mencionados, possuem a mesma medida. Mas sabemos que os ângulos opostos pelo vértice são congruentes, isto é, também possuem a mesma medida. Então, podemos dizer que:
· a = c = e = g
· b = d = f = h
Os ângulos d e f e também e e c podem ser classificados como ângulos alternos internos, pois estão na região interna e em lados alternados. Os ângulos d e e, bem como os c e f, podem ser classificados como ângulos colaterais internos, uma vez que estão na região interna e do mesmo lado em relação à reta t.
Semelhantemente, os ângulos a e h, assim como b e g, são ângulos colaterais externos, pois estão na região externa e do mesmo lado em relação à reta t. Assim como os ângulos a e g, bem como b e h, são ângulos alternos externos, pois estão na região externa e em lados alternados em relação à reta transversal t.
Na figura a seguir, podemos ver claramente os ângulos alternos internos, colaterais internos, alternos externos e colaterais externos formados através de duas retas paralelas cortadas por uma transversal:

Duas retas paralelas cortadas por uma transversal formam ângulos alternos internos, colaterais internos, alternos externos e colaterais externos
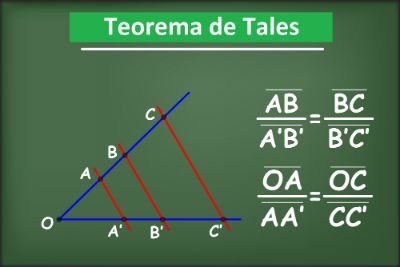
Teorema de Tales
O Teorema de Tales é uma teoria aplicada na geometria acerca do conceito relacionado entre retas paralelas e transversais.
O teorema foi desenvolvido pelo filósofo, astrônomo e matemático grego Tales de Mileto (624 a.C.- 558 a.C.) e, por isso, recebe esse nome.
O experimento de Tales foi realizado através da observação de uma sombra da pirâmide. A partir disso, ele conseguiu calcular a altura da pirâmide Quéops, no Egito, com base na sombra que ela projetava.
Considerado o “Pai da Geometria Descritiva”, Tales contribuiu para o avanço dos estudos de razão e proporção, que até os dias de hoje são utilizados para calcular distâncias.
O enunciado do Teorema de Tales é expresso pela sentença:
“a interseção entre duas retas paralelas e transversais formam segmentos proporcionais.”
Exemplo
Para compreender melhor o teorema de tales, observe a figura abaixo:
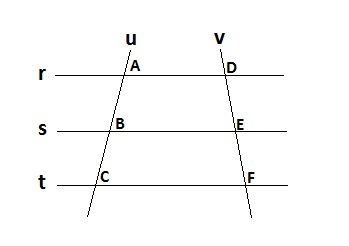
Na figura acima as retas transversais u e v interceptam as retas paralelas r, s e t. Os pontos pertencentes na reta u são: A, B e C; e na reta v, os pontos: M, N e O. Logo, de acordo com o Teorema de Tales:
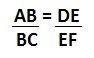
Lê-se: AB está para BC, assim como DE está para EF.
EXEMPLO:
EXERCÍCIO a:
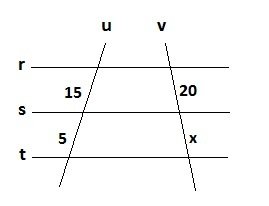
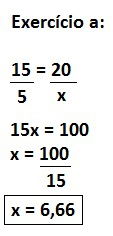


Nenhum comentário:
Postar um comentário