11-15 de Maio-Material de apoio- Retas paralelas cortadas por uma transversal-9°ano

Retas paralelas cortadas por uma transversal

Retas paralelas são aquelas que não se interceptam em nenhum ponto. Uma reta é transversal à outra se ambas apresentam apenas um ponto em comum. Ao traçarmos duas retas r e s, tal que r // s (“r é paralela a s”), e também uma reta transversal t que intercepte r e s, haverá a formação de oito ângulos. Na imagem a seguir, identificamos esses ângulos por a, b, c, d, e, f, g, h.

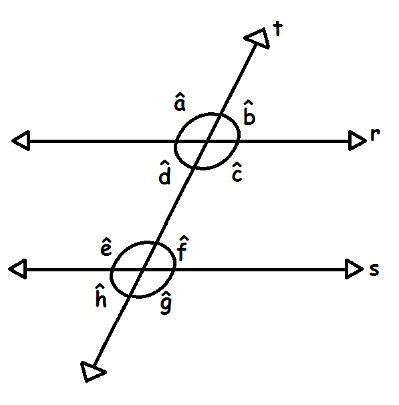
A interseção da reta t com as retas paralelas r e s deu origem aos ângulos a, b, c, d, e, f, g, h

Experimente fazer um desenho semelhante a esse que foi mostrado de duas retas paralelas cortadas por uma transversal. Ao finalizar seu desenho, divida-o ao meio, cortando-o entre as retas paralelas. Se você colocar os ângulos formados pelas retas s e t exatamente em cima dos ângulos formados pelas retas r e s, observará que eles são exatamente iguais.

Podemos classificar os ângulos formados por duas retas paralelas cortadas por uma transversal de acordo com a posição desses ângulos. Se eles estiverem entre as retas paralelas, dizemos que esses ângulos são internos; caso contrário, dizemos que eles são externos. Na figura a seguir, os ângulos externos estão na faixa azul, enquanto os ângulos internos estão na faixa amarela. Ao analisarmos dois ângulos, eles podem estar do mesmo lado ou em lados alternados em relação à reta transversal. Se dois ângulos estão à direita ou ambos estão à esquerda da reta t, dizemos que esses ângulos são colaterais; mas se estão em lados alternados, um à direita, e o outro à esquerda, dizemos que esses ângulos são alternos.

 

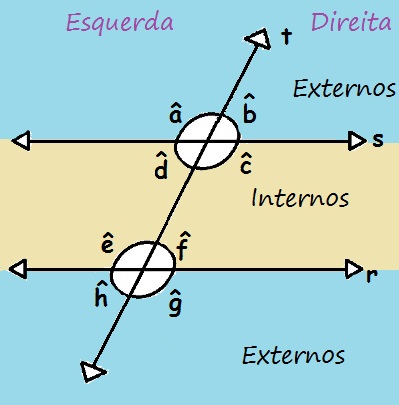
Os ângulos podem ser classificados como internos ou externos, e dois ângulos podem ser colaterais ou alternos

Sabendo que os ângulos formados pelas retas r e t são iguais aos formados pelas retas s e t, podemos afirmar que os pares de ângulos abaixo são correspondentes:

·         a e e

·         b e f

·         c e g

·         d e h

Estes pares de ângulos colaterais correspondentes, acima mencionados, possuem a mesma medida. Mas sabemos que os ângulos opostos pelo vértice são congruentes, isto é, também possuem a mesma medida. Então, podemos dizer que:

·         a = c = e = g

·         b = d = f = h

Os ângulos d e f e também e e c podem ser classificados como ângulos alternos internos, pois estão na região interna e em lados alternados. Os ângulos d e e, bem como os c e f, podem ser classificados como ângulos colaterais internos, uma vez que estão na região interna e do mesmo lado em relação à reta t.

Semelhantemente, os ângulos a e h, assim como b e g, são ângulos colaterais externos, pois estão na região externa e do mesmo lado em relação à reta t. Assim como os ângulos a e g, bem como b e h, são ângulos alternos externos, pois estão na região externa e em lados alternados em relação à reta transversal t.

Na figura a seguir, podemos ver claramente os ângulos alternos internos, colaterais internos, alternos externos e colaterais externos formados através de duas retas paralelas cortadas por uma transversal:

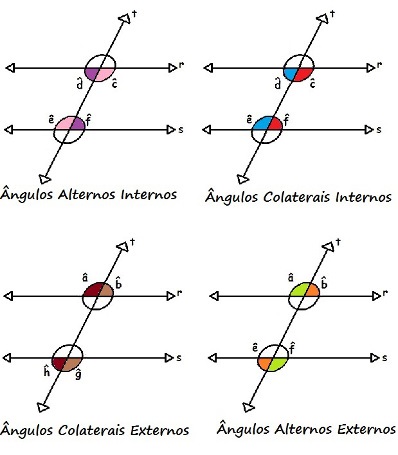
Duas retas paralelas cortadas por uma transversal formam ângulos alternos internos, colaterais internos, alternos externos e colaterais externos