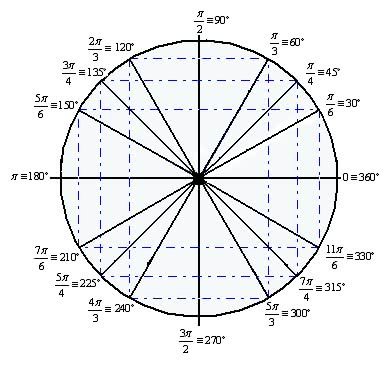
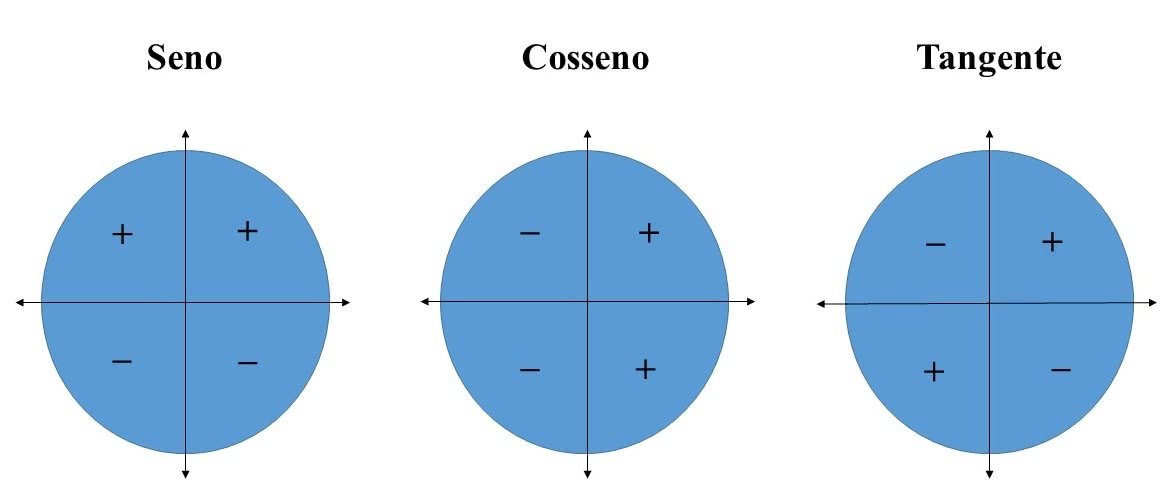
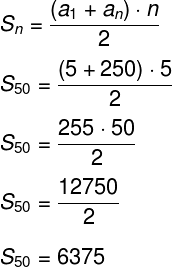PROGRESSÃO ARITMÉTICA (P.A)
A Progressão Aritmética (P.A.) é uma sequência de números onde a diferença entre dois termos consecutivos é sempre a mesma. Essa diferença constante é chamada de razão da P.A..
Sendo assim, a partir do segundo elemento da sequência, os números que surgem são resultantes da soma da constante com o valor do elemento anterior.
Isso é o que a diferencia da progressão geométrica (P.G.), pois nesta, os números são multiplicados pela razão, enquanto na progressão aritmética, eles são somados.
As progressões aritméticas podem apresentar um número determinado de termos (P.A. finita) ou um número infinito de termos (P.A. infinita).
Para indicar que uma sequência continua indefinidamente utilizamos reticências, por exemplo:
· a sequência (4, 7, 10, 13, 16, ...) é uma P.A. infinita.
· a sequência (70, 60, 50, 40, 30, 20, 10) é uma P.A. finita.
Cada termo de uma P.A. é identificado pela posição que ocupa na sequência e para representar cada termo utilizamos uma letra (normalmente a letra a) seguida de um número que indica sua posição na sequência.
Por exemplo, o termo a4 na P.A (2, 4, 6, 8, 10) é o número 8, pois é o número que ocupa a 4ª posição na sequência.
Classificação de uma P.A.
De acordo com o valor da razão, as progressões aritméticas são classificadas em:
· Constante: quando a razão for igual a zero. Por exemplo: (4, 4, 4, 4, 4...), sendo r = 0.
· Crescente: quando a razão for maior que zero. Por exemplo: (2, 4, 6, 8,10...), sendo r = 2.
· Decrescente: quando a razão for menor que zero (15, 10, 5, 0, - 5,...), sendo r = - 5
Fórmula do Termo Geral
Esse cálculo é expresso através da fórmula do termo geral da P.A., que nos permite conhecer qualquer elemento de uma progressão aritmética. Assim, temos:
an = a1 + (n - 1) . r Onde,
an : termo que queremos calcular
a1: primeiro termo da P.A.
n: posição do termo que queremos descobrir
r: razão
a1: primeiro termo da P.A.
n: posição do termo que queremos descobrir
r: razão
Exemplo
Calcule o 10° termo da P.A.: (26, 31, 36, 41, ...)
Solução
Primeiro, devemos identificar que a1 = 26, r = 31 - 26 = 5 e n = 10 (10º termo). Substituindo esses valores na fórmula do termo geral, temos:
an = a1 + (n - 1) . r
a10 = 26 + (10-1) . 5
a10 = 26 + 9 .5
a10 = 71
a10 = 26 + (10-1) . 5
a10 = 26 + 9 .5
a10 = 71
Portanto, o décimo termo da progressão aritmética indicada é igual a 71.
Sabendo que o 50º termo é 250, podemos usar a fórmula da soma dos termos para obter a soma dos 50 primeiros termos (S50) dessa PA:
SOMA DOS TERMOS DE UMA P.A
Nessa fórmula, Sn representa a soma dos termos, a1 é o primeiro termo e an é o último termo da PA em questão, n é o número de termos que serão somados. Para somar os termos de uma progressão aritmética, basta substituir os valores nessa fórmula.
EXEMPLO:
Determine a soma dos 50 primeiros termos da PA a seguir: (5, 10, 15, …).
Note que essa PA é infinita, isso é evidenciado pelas reticências. O primeiro termo é 5, assim como a razão da PA, pois 10 – 5 = 5. Como queremos descobrir a soma dos 50 primeiros termos, o 50º termo será representado por a50. Para descobrir seu valor, podemos usar a fórmula do termo geral da PA:
Nessa fórmula, r é a razão da PA. Substituindo os valores dados no enunciado nessa fórmula, teremos:
Sabendo que o 50º termo é 250, podemos usar a fórmula da soma dos termos para obter a soma dos 50 primeiros termos (S50) dessa PA:
PROGRESSÃO GEOMÉTRICA (P.G)
Progressão Geométrica (PG) corresponde a uma sequência numérica cujo quociente (q) ou razão entre um número e outro (exceto o primeiro) é sempre igual.
Em outras palavras, o número multiplicado pela razão (q) estabelecida na sequência, corresponderá ao próximo número, por exemplo:
PG: (2,4,8,16, 32, 64, 128, 256...)
No exemplo acima, podemos constatar que na razão ou quociente (q) da PG entre os números, o número que multiplicado pela razão (q) determina seu consecutivo, é o número 2:
2 . 2 = 4
4 . 2 = 8
8 . 2 = 16
16 . 2 = 32
32 . 2 = 64
64 . 2 = 128
128 . 2 = 256
Vale lembrar que a razão de uma PG é sempre constante e pode ser qualquer número racional (positivos, negativos, frações) exceto o número zero (0).
Classificação das Progressões Geométricas
De acordo com o valor da razão (q), podemos dividir as Progressões Geométricas (PG) em 4 tipos:
PG Crescente
Na PG crescente a razão é sempre positiva (q > 0) formada por números crescentes, por exemplo:
(1, 3, 9, 27, 81, ...), onde q = 3
PG Decrescente
Na PG decrescente, a razão é sempre positiva (q > 0) e diferente de zero (0) formada por números decrescentes.
Ou seja, os números da sequência são sempre menores do que seus antecessores, por exemplo:
(-1, -3, -9, -27, -81, ...) onde q = 3
PG Oscilante
Na PG oscilante, a razão é negativa (q < 0), formada por números negativos e positivos, por exemplo:
(3,-6,12,-24,48,-96,192,-384,768,...), onde q = -2
PG Constante
Na PG constante, a razão é sempre igual a 1 formada pelos mesmos números a, por exemplo:
(5, 5, 5, 5, 5, 5, 5, ...) onde q = 1
Fórmula do Termo Geral
Para encontrar qualquer elemento da PG, utiliza-se a expressão:
an = a1 . q(n-1)
Onde:
an: número que queremos obter
a1: o primeiro número da sequência
q(n-1): razão elevada ao número que queremos obter, menos 1
a1: o primeiro número da sequência
q(n-1): razão elevada ao número que queremos obter, menos 1
Assim, para identificar o termo 20 de uma PG de razão q = 2 e número inicial 2, calcula-se:
PG: (2,4,8,16, 32, 64, 128,...)
a20 = 2 . 2(20-1)
a20 = 2 . 219
a20 = 1048576
SOMA DOS TERMOS DE UMA P.G
.jpg)
EXEMPLO:
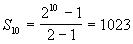
SOMA DOS TERMOS DE UMA P.G
.jpg)
EXEMPLO:
Calcule a soma dos 10 primeiros termos da PG (1,2,4,8,...)
Temos:
Temos:
Observe que neste caso a1 = 1.